Clasificatorias al mundial Rusia 2018: Una introducción a la teoría de la probabilidad.

9 de Setiembre del 2017

Las Clasificatorias están llegando a la recta final. Faltan dos fechas y la cantera de hinchas no deja de ver la tabla una y otra vez. Le quedan dos partidos a cada equipo. Son 10. ¿Cuántos resultados pueden surgir? Parece que son pocos, ¿lo serán? Cada equipo puede ganar, empatar o perder. ¡Tres estados! Lo que es mejor, vienen en pares, si un equipo gana el otro está destinado a perder y si uno empata el otro está destinado a empatar. Suena interesante: El estado de un equipo automáticamente condiciona el estado del otro. ¡No! Esto no es quantum entanglement. No te confundas. Estamos en el mundo clásico, la cuántica la dejaremos para otra oportunidad. Ahora sólo daremos nociones básicas de probabilidad.

Si en un fecha hay cinco partidos y los resultados de cada uno pueden ser 3 (ganar, perder o empatar), ¿cuántas combinaciones habrán? La respuesta es 3 x 3 x 3 x 3 x 3 = 243. Es decir, en la penúltima fecha hay 243 formas en las que puede quedar la tabla de posiciones. ¡Wow…! Eso no es todo, en la última fecha será igual. Entonces, ¿cuántas combinaciones hay en total? La respuesta es 243 x 243 = 59049. Sí, lo sé, el número es gigantesco y eso que no hemos considerado el número de goles.
El objetivo es reducir este número para poder estudiarlo y así determinar quienes serán los cinco clasificados (en este artículo, cada vez que hablemos de un equipo clasificado estamos incluyendo el puesto de repechaje). Veamos los partidos a jugar,

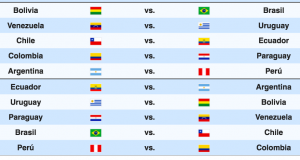
Prestemos atención al partido Bolivia vs Brasil. ¿El resultado alterará la tabla de posiciones?

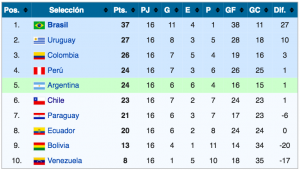¡Claro que no! Brasil va primero y Bolivia casi último. Podemos decir entonces que así Bolivia golee 5-0 la tabla de posiciones no cambiará. Por consiguiente, la penúltima fecha sólo cuenta con 4 partidos importantes. Siguiendo los cálculos hechos inicialmente procedemos,

• Combinaciones posibles en la penúltima fecha: 3 x 3 x 3 x 3 = 81
• Combinaciones posibles en la última fecha: 3 x 3 x 3 x 3 x 3= 243
• Total de Combinaciones posibles: 81 x 243 = 19683

¡Wow…! Ya no son 59049 casos sino 19683. Vamos por buen camino. ¿Qué más podemos hacer? Veamos los partidos de Uruguay. Juega contra Venezuela en Caracas y contra Bolivia en Montevideo. Además, su diferencia de goles es la más alta (excluyendo a Brasil). Basta que gane uno de esos dos partidos para estar en el mundial. Inclusive, basta que empate uno para clasificar. Es asequible, demasiado fácil. Por tanto, vamos a asumir sin miedo a equivocarnos que Uruguay ya está clasificado y sus rivales, Bolivia y Venezuela, así ganen, no modificarán la tabla de posiciones. Por tanto, en la penúltima fecha sólo hay 3 partidos trascendentales y en la última sólo 4. Tenemos,

• Combinaciones posibles en la penúltima fecha: 3 x 3 x 3 = 27
• Combinaciones posibles en la última fecha: 3 x 3 x 3 x 3 = 81
• Total de Combinaciones posibles: 27 x 81 = 2187

¡Wow…! Ya no son 19683 casos sino 2187. Entre los partidos que quedan hay uno que marca un antes y un después en el desenlace de las Clasificatorias. Es el partido de Colombia vs Paraguay. Si Paraguay gana tendríamos que analizar 2187 casos porque Colombia, yendo tercero, podría quedar fuera del mundial. Este caso será analizado en un próximo artículo y quedará excluido del presente análisis. Más adelante estudiaremos el caso en que empatan. Por ahora vamos a considerar que Colombia gana en Barranquilla, entonces elimina a Paraguay y queda clasificado (más adelante verificaremos esta premisa). ¿Cuántos casos quedan por analizar? Al Colombia ganar, el partido de Paraguay frente a Venezuela es irrelevante, por tanto, sólo tenemos dos partidos trascendentales en la penúltima fecha y tres en la última. Esto nos da,

• Combinaciones posibles en la penúltima fecha: 3 x 3 = 9
• Combinaciones posibles en la última fecha: 3 x 3 x 3  = 27
• Total de Combinaciones posibles: 9 x 27 = 243

¡Así es! Teniendo a Colombia como vencedor nos quedan 243 combinaciones. De todas ellas sólo una representará el final de las Clasificatorias. En este análisis tenemos tres clasificados: Brasil, Uruguay y Colombia. Los aspirantes a los dos cupos que faltan son Ecuador, Chile, Argentina y Perú. Sus partidos son los siguientes,

Chile vs Ecuador
Argentina vs Perú

Ecuador vs Argentina
Perú vs ———
——— vs Chile

Como ves, en la última fecha no importa mucho quienes sean los rivales de Perú y Chile porque los únicos que pueden alterar la tabla de posiciones son ellos y no sus rivales. 243 ya es un número manejable. Ahora haremos uso de la teoría de  la probabilidad para saber que equipos son favoritos “matemáticamente.” Aquí no estamos hablando de favoritos porque en las últimas Clasificatorias siempre ganaron, o porque están ahora en un buen puesto en el ranking FIFA, o porque juegan de local y sus chances son altas. ¡No! Aquí el resultado es puramente matemático y las conclusiones van más allá de lo que la intuición o la creencia puedan dictaminar. Precisamente así nació la teoría de la probabilidad. En sus inicios se creía que el azar estaba determinado por un ser superior, que si uno lanzaba los dados y salía un seis era porque estaba destinado a salir ese número. Con los años, las matemáticas fueron superando a las creencias, hombres como Cardano, Galileo, Pascal y Fermat colocaron los primeros cimientos de la teoría de la probabilidad, que en forma sencilla indica que las chances de que suceda un evento de un total de N casos posibles igualmente probables es igual a la razón entre el número de ocurrencias n de dicho evento (casos favorables) y el número total de casos posibles, es decir, n/N. Veamos algunos ejemplos sencillos con las Clasificatorias.

¿Cuál es la probabilidad que un equipo gane su partido?
P = 1/3 = 33.3%

¿Cuál es la probabilidad que Argentina le gane a Perú y al mismo tiempo Chile le gane a Ecuador?
P() ∩ P() = 1/3 x 1/3 = 1/9 = 11.1%

Como un equipo sólo puede ganar, perder o empatar, entonces la probabilidad de ganar es 1 de 3. Y como los partidos de Argentina y Chile son resultados independientes, la probabilidad total viene dada por su multiplicación, 1 de 9. Este número además nos indica que hay nueve formas en las que Argentina vs Perú y Chile vs Ecuador pueden agruparse. Los cuales son,

A) Chile vs Ecuador (GP) – Argentina vs Peru (GP)
B) Chile vs Ecuador (EE) – Argentina vs Peru (GP)
C) Chile vs Ecuador (PG) – Argentina vs Peru (GP)
D) Chile vs Ecuador (GP) – Argentina vs Peru (EE)
E) Chile vs Ecuador (EE) – Argentina vs Peru (EE)
F) Chile vs Ecuador (PG) – Argentina vs Peru (EE)
G) Chile vs Ecuador (GP) – Argentina vs Peru (PG)
H) Chile vs Ecuador (EE) – Argentina vs Peru (PG)
I) Chile vs Ecuador (PG) – Argentina vs Peru (PG)

Cada sub-grupo (o conjunto) está etiquetado con las letras de la A a la I. GP indica que el ganador es el equipo local y el perdedor el visitante, EE indica que ambos empatan y PG indica que el perdedor es el equipo local y el ganador el visitante.

¿Cuál es la probabilidad de obtener H?
P(H) = 1/9 = 11.1%

¿En la última fecha qué puede ocurrir? Hay 27 posibles consecuencias para cada sub-grupo. Los resultados aparecen detallados en el anexo. Click aquí para que veas las 243 combinaciones posibles.  

¿Cuál es la probabilidad de obtener A y luego que Perú le gane a Colombia?
P(A) ∩ P() = 1/9 x 9/27 = 9/243 = 3.7%

Habiendo estudiado los datos mostrados en el anexo, las conclusiones más interesantes que arroja la teoría de la probabilidad son,

I. Los resultados se definen por diferencia de goles

Basta mirar las Tablas A.2, B.2, C.2, D.2, E.2, F.2, G.2, H.2 e I.2 en la información suplementaria. Uno puede apreciar que la probabilidad de clasificar de muchos equipos se incrementa considerablemente sólo por tener mejor diferencia de goles. Esto es de esperar pues a la fecha Argentina, Chile y Perú tienen casi el mismo puntaje, y lo que es peor, tienen la misma diferencia de goles. Por consiguiente, el equipo que logre ganar por más de dos goles podría incrementar considerablemente sus chances de llegar al mundial. Y el equipo que pierda por más de dos goles podría perjudicar notablemente sus chances de clasificar.

II. A Perú le basta ganar a Argentina para estar (casi) clasificado

Veamos los resultados del sub-grupo G donde Perú le gana a Argentina y Chile le gana a Ecuador,

Tabla G.2

Probabilidad de clasificación	Si Brasil le gana a Chile	Si Brasil empata con Chile	Si Brasil pierde con Chile
	3/9	0 (3/9)	0 (1/9)
	9/9	8/9 (9/9)	8/9 (9/9)
	0	0	0
	6/9	6/9 (9/9)	9/9

Como se aprecia en la Tabla G.2, así Chile gane sus dos partidos, la probabilidad de clasificación de Perú oscila entre el 89% y 100% y eso que estamos considerando que Perú pierde contra Colombia. Los valores en paréntesis muestran la probabilidad en caso el equipo tenga la mejor diferencia de goles. Por ende, Perú clasifica si o si siempre y cuando le gane a Argentina  por una diferencia de dos goles (asumiendo que los demás ganan por 1).

¿Qué pasa si Perú empata con Argentina? Los resultados del sub-grupo D arrojan,

Tabla D.2

Probabilidad de clasificación	Si Brasil le gana a Chile	Si Brasil empata con Chile	Si Brasil pierde con Chile
	4/9 (7/9)	4/9 (6/9)	3/9 (6/9)
	4/9 (7/9)	4/9 (6/9)	3/9 (6/9)
	0	0	0
	5/9 (8/9)	8/9	9/9

Tal como se muestra en la Tabla D.2, empatando con Argentina, para el caso específico en que Chile le gana a Ecuador, la probabilidad de clasificación de Perú oscila entre 3/9 y 4/9. No obstante, sus chances se incrementan hasta 7/9 si obtiene la mejor diferencia de goles, es decir, si mete muchos goles a Colombia en su último partido. Por consiguiente, para no depender de muchas variables, Perú sólo debe enfocarse en ganarle a Argentina en la Bombonera y así olvidarse de Colombia.

III. Argentina sólo necesita ganarle a Perú para estar (casi) clasificado.

Al igual que Perú, las chances de Argentina son muy altas. Consideremos los resultados del sub-grupo A, donde Argentina le gana a Perú y Chile le gana a Ecuador,

Tabla A.2

Probabilidad de clasificación	Si Brasil le gana a Chile	Si Brasil empata con Chile	Si Brasil pierde con Chile
	9/9	8/9 (9/9)	8/9 (9/9)
	3/9	0 (3/9)	0 (1/9)
	0	0	0
	6/9	6/9 (9/9)	9/9

En este caso, así Chile le gane a Brasil, la probabilidad de clasificar de Argentina oscila entre 8/9 y 9/9. Cabe resaltar que el perdedor del duelo Argentina vs Perú reduce sus chances de clasificar hasta un máximo de 3/9 (ver Tablas A.2 y G.2). Por tanto, podemos concluir que este duelo es un partido trascendental donde el ganador, sin importar lo que ocurra en los otros partidos, sin importar que pierda en la última fecha, está prácticamente clasificado… y el perdedor no tendrá otra que disputar el último cupo con Chile (si es que vence a Ecuador).

IV. Chile depende de sus goles

Como se aprecia en las Tablas mostradas anteriormente (A.2, D.2, G.2), si Chile golea a Ecuador su probabilidad de clasificación aumenta considerablemente y no importa mucho el resultado de Argentina vs Perú, porque independientemente de este, su probabilidad de clasificación se ubica por encima de uno o los dos equipos.

V. Ecuador está al filo del abismo

Ecuador puede sobrevivir ganándole a Chile. Al hacerlo, su probabilidad de clasificación puede llegar a 3/9 = 33.3%. Lo curioso es que si empata también tiene chances de hacerlo, pero debe esperar que Perú le gane a Argentina y en su última fecha debe golear (ver Tabla H.1 en la información suplementaria). Si pierde en Santiago quedará eliminado y le dirá adiós al mundial.

Respondamos ahora las siguientes preguntas:

1. ¿Qué pasa si Colombia empata con Paraguay?

El puntaje de repechaje oscila entre 24 y 29 puntos (en la siguiente pregunta detallamos estos números), lo que demuestra que Colombia ganando a Paraguay está clasificado. En caso de empate Colombia haría 27 puntos (perdiendo con Perú en la última fecha) y Paraguay llegaría a 25 (ganándole a Venezuela en la última fecha). Dentro de todas las combinaciones mostradas en el anexo, el puntaje más alto del “mejor eliminado” es de 28 puntos, pero sólo ocurre una vez entre las 243 posibilidades. Se da cuando Argentina y Perú empatan en la penúltima fecha  y todos ganan (menos Ecuador) en la última fecha. Si esto no se cumple, Colombia estaría casi clasificado, y digo casi porque existen 20 combinaciones de las 243 posibles en las cuales el mejor eliminado obtiene 27 puntos, los mismos puntos que Colombia. Por tanto, la clasificación dependerá de la diferencia de goles y para suerte de los parceros ellos llegan bien en ese aspecto al tener una cifra superior a la de sus rivales. Consecuentemente, la probabilidad de clasificación de Colombia es muy alta así pierda con Perú y empate con Paraguay.

Paraguay por su parte, empatando con Colombia y ganando a Venezuela llegaría a 25 puntos como máximo, con estos podría luchar por la clasificación. No obstante, recordemos que Paraguay tiene una diferencia de goles de -6. Para disputar un puesto con ese puntaje debe golear 7-0 a Venezuela. Algo difícil de imaginar. Lo más asequible es pensar en la probabilidad que tiene Paraguay de alcanzar el cupo de repechaje directamente, es decir, ver en cuantos casos el cupo se alcanza con 24 puntos para así poder superarlo con sus 25 puntos dables. Esto nos lleva a responder antes la siguiente pregunta.

2. ¿Cuál es el puntaje de repechaje más probable?

Para esto emplearemos el diagrama del árbol. Existen 9 sub-grupos (de la A a la I) y en cada uno tenemos las siguientes probabilidades para los puntajes de repechaje (ver Tablas A.3, B.3, C.3, D.3, E.3, F.3, G.3, H.3 e I.3 en la información suplementaria):

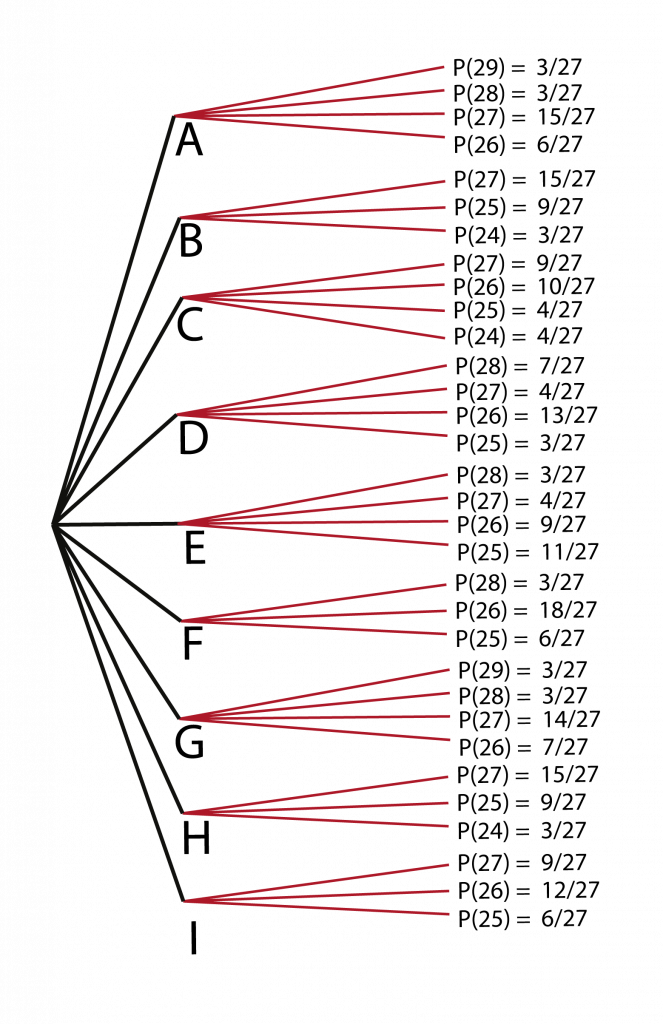Por ejemplo, P(29) indica la probabilidad de obtener 29 puntos en el puesto de repechaje.

¿Cuál es la probabilidad de obtener, a través de A, 29 puntos en el puesto de repechaje?
P(A ∩ 29)=P(A) x P(29/A) = 1/9 x 3/27 = 3/243 = 1.2%.

Esto se conoce como una probabilidad condicionada porque queremos hallar un valor condicionándolo a que salga por una de las ramas del árbol. Su resultado viene dado por la probabilidad de obtener A multiplicado por la probabilidad de obtener 29 puntos en A. Se suele denotar P(A ∩ 29). Entonces, la probabilidad total de obtener 29 a través de todas las ramas vendría a ser la suma de cada una de ellas, i.e., P(29) = P(A ∩ 29) + P(B ∩ 29) + P(C ∩ 29) + P(D ∩ 29) + P(E ∩ 29) + P(F ∩ 29) + P(G ∩ 29) + P(H ∩ 29) + P(I ∩ 29). Haciendo esto para todos los valores obtenemos:

P(29) = 6/243
P(28) = 19/243
P(27) = 85/243
P(26) = 75/243
P(25) = 48/243
P(24) = 10/243

Por ende, lo más probable es que el 5to puesto en las Clasificatorias obtenga 26 o 27 puntos, i.e., P(26) = 75/243 = 30.9% y P(27) = 85/243 = 35%. De aquí podemos culminar la respuesta anterior. Dijimos que a Paraguay, más que meter 7 goles a Venezuela le conviene alcanzar el cupo de repechaje directamente. Es decir, las chances de Paraguay se reducen a P(24) = 10/243 = 4%. Una probabilidad tan baja que es mejor aceptar la realidad de decirle adiós al mundial. Por lo expuesto, un empate entre Colombia y Paraguay no afecta en gran medida los resultados mostrados en este artículo.
En un inicio dijimos que Uruguay estaría clasificado haciendo un punto en sus dos últimos partidos. Si esto ocurre Uruguay llegaría a 28 puntos con una diferencia de goles muy superior a los demás. Por consiguiente, vemos que su probabilidad de quedar eliminado es de P(29) = 6/243 = 2.5%. Lo curioso es que para que esto ocurra Chile debe ganarle a Brasil. Por tanto, sacar un punto en dos partidos no debería causar ninguna preocupación a los uruguayos.

3. ¿Quiénes serán los 5 clasificados?

Las matemáticas indican que Argentina, Chile y Perú son los candidatos a pelear los cupos que faltan. ¿Quién llevará sus cánticos al mundial? ¿Cantará Chile, “prepárate Rusia que aquí vamos por más”? O Perú gritará, “porque yo creo en ti, ¡vamos vamos Perú!” O será Argentina quien dirá, “esta barra quilombera no te deja de alentar.” La probabilidad total que tiene cada equipo de clasificar (antes de jugarse las dos últimas fechas) es,

El análisis es similar al diagrama del árbol desarrollado previamente, aquí sólo mostramos los resultados por simplicidad (basados en los datos de las Tablas A.2, B.2, C.2, D.2, E.2, F.2, G.2, H.2, I.2 en la información suplementaria). Lo interesante es que a pesar que Argentina y Perú tienen el mismo puntaje antes de jugar sus partidos, al culminarlos, la probabilidad de clasificación de Perú es mayor. Esto se explica porque Argentina juega con rivales directos en ambas fechas, mientras que Perú en la última fecha lo hace con un equipo “clasificado.” Otro detalle interesante es ver cómo afecta tener la mejor diferencia de goles. Chile resulta ser el más beneficiado, incrementando su probabilidad de clasificación en 18.1 puntos porcentuales sólo por meter más goles. En contraste, Perú y Argentina incrementan su probabilidad de clasificación en 15.3 y 13.6 puntos porcentuales, respectivamente. Por tanto, para hacer uso de esta ventaja, los chilenos deberían enfocarse en golear a Ecuador en casa. De todas formas Chile tiene la probabilidad más baja de clasificación (excluyendo a Ecuador), y eso que estamos incluyendo el caso en que le pueda ganar a Brasil. Si consideramos que estos resultados son determinantes, podemos concluir que los 5 equipos clasificados serán: Brasil, Uruguay, Colombia, Perú y Argentina. La pregunta pendiente sería ¿qué equipo clasifica directamente al mundial? ¿Perú o Argentina? Realizando un análisis similar al anterior tenemos:

Probabilidad de coger el cupo directo al mundial

Con la mejor diferencia de goles	Con la peor diferencia de goles
P() = 121/243 =  49.8% P() = 121/243 =  49.8%	P() = 83/243 = 34.2% P() = 81/243 = 33.3%

Argentina obtiene una probabilidad ligeramente superior de clasificar directamente al Mundial. La razón es la misma que el caso anterior y toma relevancia en el sub-grupo F (ver información suplementaria). Si esta ligera ventaja fuese un factor determinante, Perú terminaría enfrentando a Nueva Zelanda el 11 de noviembre. Los dirigidos por Gareca se subirían al avión y harían el viaje más bizarro de sus vidas. Cruzarían el Pacífico en un viaje que el reloj desde Santiago les diría que son 12 pero tardarían 27 horas en llegar y la vuelta desde Auckland la harían con el tiempo transcurriendo con valores negativos, pero eso no les importaría… porque España 82′ finalmente podría quedar atrás.

Christian Ortiz, PhD.