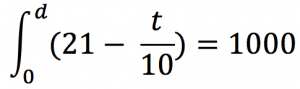Author’s note: “This article was published on August 4th, 2017. Considering Integral Calculus we predicted that Despacito would reach 4 billion views in october 2017 and 5 billion views in april 2018. Officially Despacito reached 4 billion views on october 11th 2017 and 5 billion views on april 4th 2018.”
Despacito will reach 4 billion views this year and…
In the first part of this article, published on July 11th, 2017, using basic mathematical notions we predicted that Despacito would reach 3 billion views after August 2nd, with a strong probability on the threshold of the second week. Officially it happened on August 4th in America and on August 5th in Europe and Asia. The route taken was as follow (UTC +2):
- Surpassed Uptown funk – Bruno Mars, on July 14th, 2017 at 7:30 PM.
- Surpassed Sorry – Justin Bieber, on July 19th, 2017 at 11:30 AM.
- Surpassed Gangnam style – PSY, on July 31st at 5:00 PM.
- Surpassed See you again – Wiz Khalifa on August 4th at 7:30 PM.
- Reached 3 billion views on August 5th at 00:30 AM.
In this second part, we are going to answer when will it reach 4 billion views and be considered the only song achieving this number. The answer, once again, lies in mathematics…
Despacito started growing at 6 million views per day in January, increased its rate to 16 million views per day in May, and reached 21 million views per day in July. Will it reach higher values? No, it will not, Despacito will decay reaching a stable level in January 2018 (6 months after reaching its highest peak, which was in July), this is likely to happen because other songs have shown this outcome. What would this stable value be? Probably around 3 million views per day. Why? Because it has been the stable value of many iconic songs. Here are some examples:
| Song / Artist | Published in Youtube (year/month) | Number of Youtube views per day in 2017/08 (millions) |
| Bailando (Enrique Iglesias) |
2014/04 | 2 |
| Uptown funk (Bruno Mars) | 2014 /11 | 2 |
| Sorry (Justin Bieber) |
2015 /10 | 2 |
| See you again (Wiz Khalifa) |
2015/04 | 3.5 |
| Chantaje (Shakira) |
2016/11 | 4.5 |
This data wil be enough to make a rough estimation of the future of the song using Integral Calculus (developed by Isaac Newton and Gottfried Leibniz in the XVII century). Probably in that time, these geniuses had to face a similar problem and that’s how they developed Calculus, so let’s go back in time and see what they would have done…
First, Newton would have locked himself in his room, he was a shy person and preferred solitude. Then, he would have drawn a graph similar to the following:
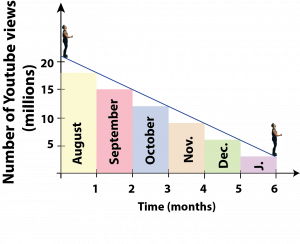
Showing that in 6 months (from August 2017 to January 2018) Despacito would fall linearly from 21 million to 3 million views per day (see blue line in Figure 1), reaching a stable and constant value starting february. With this, knowing that beginning august Despacito has 3 billion views, can we derive when will it reach 4 billion views? It looks a bit cumbersome, because of this, Newton and Leibniz developed a trick… Instead of studying the line, they traced rectangles for each month as shown in Figure 1. Why? Because by doing so, things become much simpler, we now can assume that in August Despacito would have a constant value of 18 million views per day, in September of 15 million views per day, in October 12, in November 9, in December 6, and in January 3; hence, considering that each month has 30 days we can generate the following table:
| Month | Total number of Youtube views each month (millions) |
| August | 18 x 30 = 540 |
| September | 15 x 30 = 450 |
| October | 12 x 30 = 360 |
| November | 9 x 30 = 270 |
| December | 6 x 30 = 180 |
| January | 3 x 30 = 90 |
| Total | 1890 |
From the table we can see that adding August and September, Despacito accumulates 990 million views, meaning that it would require only 10 million to reach 4 billion views in total. And by the end of January, it would reach 4.890 billion views, requiring then 110 million to reach 5 billion views in total. Taking into account the exact date in which Despacito accumulated 3 billion views and assuming that after January it keeps a stable value of 3 million views per day we can conclude that:
-
- Despacito reaches 4 billion views on October 5th, 2017.
-
- Despacito reaches 5 billion views on March 12th,, 2018.
These dates do not correspond to the blue line but instead to the approximation given by the rectangles. The curious thing about this trick is that the area of each rectangle shown in Figure 1 represents the total number of views in each month, eg, for August, the width of the rectangle is 30 (days) and the length is 18 (number of views per day), then the total number of views is 30 x 18, as shown in the table above. Oh God!-would have said Newton, who was a fervent Christian, while pulling his hair in his little dorm in Woolsthorpe. Leibniz would have done the same in Paris.
Both were fascinated with the concept of the infinitesimal, to the point that they were immersed in philosophical debates regarding the so called monads. Because of this, both reached a point where they questioned themselves: “what if we draw more rectangles and make them thinner, infinitesimally thinner so that they would exactly match the area under the curve (the blue line in our case).” This simple thought gave a marvelous conclusion: “The area under the curve, no matter how complicated is this curve, gives us the total number views.”
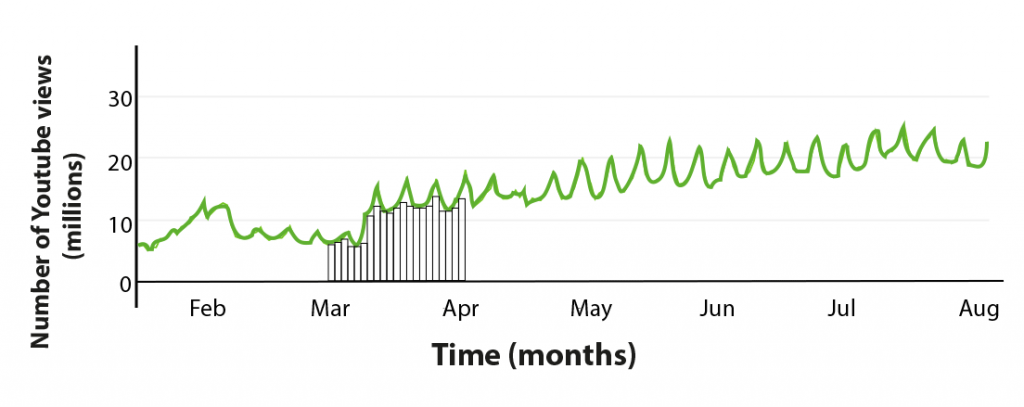
To visualize this thought, let’s consider Figure 2, where we show the actual evolution of the number of views of Despacito from January to August, 2017. As you can see, the behavior is not linear, but Newton and Leibniz showed us that in order to get the total number of views, all we need is to find the area under the curve (the area under the green line in this case). By drawing thin rectangles in the month of March (as shown in Fig. 2) and summing up their areas we can obtain approximately the total number of views in that month. The value will be exact if these rectangles are infinitesimally thin, so thin that when they are drawn they describe exactly the area under the curve. This conclusion allowed them to develop Integral Calculus, which in simple words means: “To find the total area under any curve we just need to sum up the area of infinitesimally thin rectangles.” For this it is necessary to know the equation of our curve. In Fig. 1 is a straight line, its general form was mentioned in the first part of this article. In Fig. 2 is more complex but not impossible to determine. In this case we are going to center our attention in Fig. 1, the equation of the straight line is given by the function f(t) = 21 – t/10, where t represents the time expressed in days. This function will allow us to obtain the length of the rectangle and the width will be given by an infinitesimally small value. Therefore, we already have the area of each rectangle and all we need is to sum them up. Mathematically, this infinitesimal sum is expressed as follows:
On the left hand side we have the equation of our line, f(t). The symbol in the form of an elongated S tells us that we have to add infinitesimally thin rectangles starting on day 0 and culminating on day d, date for which we will accumulate 1 billion views. Solving the equation we have:
-
- Despacito reaches 4 billion views on September 30th, 2017.
-
- Despacito reaches 5 billion views on January 1st, 2018.
How accurate are these results?
With time we will know, Despacito may decay faster (or slower) than a linear slope, in fact, it will be a chaotic decay, very similar to Fig. 2. We are just making a rough approximation, but everything seems to indicate that the first week of October Despacito will reach 4 billion views and between January and April, 2018, Despacito will grasp 5 billion views. The imminent question is: Is any song capable of beating this record? It is very difficult at the moment. The great advantage of new songs coming by is that the global connection to the internet is increasing; however, if the world population is meant to decrease for any reason in the coming years, most likely Despacito will remain unbeaten for a long long time.
Christian Ortiz, PhD.